A Fast and Hardware-Friendly Surface Tessellation Method

Here is some tessellation code I've written in 2002. At that time, I didn't find any useful resource so I had to probably reinvent the wheel. Anyway, it might save you some time if you found this blog while searching for «example tessellation code». This is adapted from the method I used in my Catmull-Rom subdivision surfaces code.

Consider the following patch which has been tesselated to a 3x4 regular grid and turned into a triangle strip:

I define each patch to be a quad that covers the [0..1]x[0..1] region of (u,v)=R². So it's bound by 0<=u<=1 and 0<=v<1. Let's call this the Grid Space.

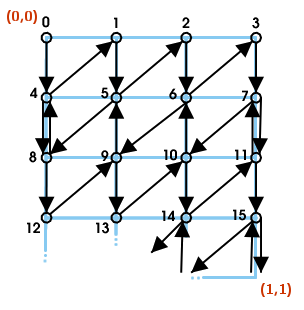
Here is a linearized version showing each vertex's index:

I use a vertex buffer containing all my vertices, and an index buffer referencing those vertices.

So, if we put [0, 4, 1, 5, 2, 6, 3, 7, 11, 7, 10, 6, 9, 5, 8, 4, 8, 12, 9, 13, 10, 14, 11, 15, ...] in an index buffer, we can use it to reference our grid as a triangle strip.

Here are some pre-declarations:

// vector_t holds vertex coordinates in whatever format you may like
// (I use a GL_T2F_V3F interleaved format for mine)
class vector_t;

// A vertex Buffer class (basically an array of vector_t)
class vertex_buffer_t;

// An index Buffer class (basically an array of unsigned ints)
class index_buffer_t;

And this is some pseudo code for filling the buffers:

fill_vertex_buffer(vertex_buffer, u_segments, v_segments) {
   for (v=0; v<v_segments; ++v) {
      for (u=0; u<u_segments; ++u) {
         with vertex_buffer[u + v*(u_segments+1)] {
            // define a quad in model space:
            .x = (float)u/(float)u_segments;
            .y = (float)v/(float)v_segments;
            .z = .0f;
         }
      }
   }
}

fill_index_buffer(index_buffer, u_segments, v_segments) {
   // For u_segments = 3 and v_segments>3, the result will be:
   // [0, 4, 1, 5, 2, 6, 3, 7, 11, 7, 10, 6, 9, 5, 8, 4, 8, 12, 9, 13, 10, 14, 11, 15, ...]
   // local variables:
   u_vertex_stride = u_segments+1; // =4: if x is the Nth vertex of a row, x+4 is the Nth vertex on the next.
   index_count = (u_vertex_stride*v_segments)*2; // = we will generate an index buffer with 32 indices.
   u_twice_vertex_stride = u_vertex_stride*2;

   // fill the index buffer:
   for (index=0; index<index_count; ++index) {
      // x-coordinate in tesselated grid-space:
      x = (index/2)%u_twice_vertex_stride;
      if (x>=u_vertex_stride) x=(u_twice_vertex_stride-1)-x;
      // y-coordinate in tesselated grid-space:
      y = index/u_twice_vertex_stride;
      if (index&1 ^ y&1) ++y;
      // Index of the vertex in the vertex buffer:
      index_buffer[index] = y*u_vertex_stride + x;
   }
}

Now, this fill_vertex_buffer() function is quite useless, since we do not want to tesselate a single quad, but more likely a subdivision surface described by some function.

Here is a surface function declaration:

// A function of surface_function_t  type returns a vector_t
// which is function of two parameters u and v, whose value is between 0 and 1.
// In order to be called a surface, such function must be continuous in [0 .. 1]².
typedef vector_t (*surface_function_t)(float u, float v);

Ok, now here is the tesselator that subdivides and samples a surface along a u_segments x v_segments grid in [0..1] x [0..1] range and produces a triangle strip representing the resulting sampled surface in the given vertex/index buffers:

void tesselate(
   surface_function_t surface,
   vertex_buffer_t& vertex_buffer,
   index_buffer_t& index_buffer,
   unsigned short u_segments,
   unsigned short v_segments) {

   // Reserve enough space
   vertex_buffer.reserve((u_segments+1)*(v_segments+1));

   // Declare loop increments
   const float u_inc(1.f / (float)u_segments));
   const float v_inc(1.f / (float)v_segments));

   // Compute surface points
   float v=.0f;
   for (unsigned short v_step=0; v_step<=v_segments; ++v_step) {
      float u=.0f;
      for (unsigned short u_step=0; u_step<=u_segments; ++u_step) {
         vertex_buffer[v_step*(u_segments+1) + u_step] = surface(u,v);
         u += u_inc;
      }
      v += v_inc;
   }

   // Fill the index buffer with indices automagically forming a single triangle strip:
   unsigned int u_vertex_stride = ((unsigned int)u_segments)+1;
   unsigned int index_count = (unsigned int)(u_vertex_stride*v_segments<<1);
   unsigned int u_twice_vertex_stride = u_vertex_stride<<1;
   index_buffer.reserve(index_count);
   for (unsigned int index=0; index<index_count; ++index) {
      unsigned int x,y;
      x = (index>>1)%u_twice_vertex_stride;
      if (x>=u_vertex_stride) x=(u_twice_vertex_stride-1)-x;
      y = index/u_twice_vertex_stride;
      if (index&1 ^ y&1) ++y;
      index_buffer[index] = y*u_vertex_stride + x;
   }
}